- de
- en
Table of Contents
Immediately Show Questions when a Certain Option is Selected
Filters allow content or questions to be shown depending on previous answers – however, sometimes an additional question should appear directly on the same questionnaire page. This is known as dynamic content because the display changes without a new HTML page being transmitted by the browser. Dynamic changes require JavaScript: a programming language that runs in the participant's browser. The server does not undergo any of the changes at first; it only receives the responses after the participant clicks on “next”.
Generally speaking, extensive modificitions within a questionnaire page are possible with JavaScript and the Document Object Model (DOM). However, sometimes this requires advanced programming knowledge. This manual is limited to how a question is shown or hidden depending on an answer.
Tip: If the JavaScript code doesn't work right away, please use the Developer Tools in the Browser for troubleshooting.
The Basics
- In JavaScript there are Event Handler. These are functions that are triggered by the user's actions on the page. The actions generate an Event, and this triggers the associated JavaScript function, the EventHandler. Possible events are …
'click'– the click on an element,'mouseover'– moving the mouse over an element,'change'– selecting an option in a dropdown or changing a text input field,'keypressed'– a keystroke- and many others.
- Each element of an (HTML) internet page has a whole range of properties. SoSci Survey creates the individual questionnaire pages as HTML pages – and all questions and input fields are HTML elements, whose properties can be shaped by JavaScript. One of these properties is the display style (
style) and the display mode (display) is a part of this. The display mode defines how an element is shown (blockorinline), or that it simply should not be shown at all (none). - The elements of an HTML page can be addressed most simply by referring to their HTML ID. SoSci assigns HTML IDs automatically for all input fields that are focused on the question/item ID.
- The simplest way to generate an element's ID is for you to use the Developer Tools in the Browser. These tools can show you the HTML code of an element (e.g. a selection field) – incl. the HTML ID (
id="AB01_01"). Alternatively, you can display the source code of the HTML page in the browser and look for the corresponding element there. - SoSci assigns an HTML ID to each question consisting of the question ID, an underscore, (
_) andqst(e.g.AB01_qstfor question “AB01”).
- In SoSci Survey, any content can be incorporated into a questionnaire page. Therefore, this includes JavaScript code. The easiest way of doing this is to save the code as a text element in Text Elements and Labels(for the display you have to select “HTML-Code”) and dragging and dropping this text element into the page in Compose Questionnaire and into the respective question(s).
Note: The user has to be (invisible) on the page in order to insert questions dynamically. Do not insert/hide compulsory questions: even if the participant cannot answer hidden questions, SoSci Survey insists on a response for compulsory questions.
Note: The JavaScript code should be designed to hide unnecessary content; not show necessary content. This has the advantage that participants with JavaScript deactivated can still answer the question as the question was not hidden.
Note: Screenreaders, which enable people with visual impairments to take part in your survey, do not always cope with dynamic content. Using this feature can reduce the accessibility of your questionnaire.
Note: Some question types use a different display for each screen by default (responsive layout). In rare cases, the display is not selected correctly when you display such a question via JavaScript. In this case, please set another option than “dynamic” for display in the question.
Note: If you use a simple selection or scale (i.e. no multiple selection) as a filter question and you have activated the option Deselect checkbox in simple selection or scale in the questionnaire, the property checked will still return true instead of false after deselecting an option. In this case, use the event change instead of click.
Tip: If the participant sees that one of the selection options involves extra work, then this could influence his responsiveness. Here, a classic Filter asking the second question on the following page could make more sense.
Example 1: Visible Selection
Depending on a yes/maybe/no question (“JN01”, visible selection), a text question (“TX01”) should be shown.
The following JavaScript code is saved as a text element (display: “HTML-Code”), dragged and dropped below questions “JN01” and “TX01” in the questionnaire page.
<script type="text/javascript"> <!-- var optionA = document.getElementById("JN01_01a"); // JN01_01a is the HTML ID of the selection option "yes" var optionB = document.getElementById("JN01_02a"); // "maybe" option var optionC = document.getElementById("JN01_03a"); // "no" option var question = document.getElementById("TX01_qst"); // HTML ID of the text input function toogle() { // the two pipes (||) are a logicial "or" // the condition checks: is option A selected or is B selected? if (optionA.checked || optionB.checked) { // if "yes" or "maybe" is selected, then the question is shown // no input ("") uses the default setting (display as usual) question.style.display = ""; } else { // question is hidden if the "none" option is selected question.style.display = "none"; } } // The function should always be executed, if one of the three options is clicked on SoSciTools.attachEvent(optionA, "click", toogle); SoSciTools.attachEvent(optionB, "click", toogle); SoSciTools.attachEvent(optionC, "click", toogle); // and the function should also be executed, so that the display at the beginning is correct // (e.g. hide the text input at the beginning) toogle(); // --> </script>
Example 2: Drop-down
An additional question (“DD02”“) should be shown depending on whether a certain option (e.g. those with the answer code “7”) was selected in a drop-down selection (“DD01”).
<script type="text/javascript"> <!-- var dropdown = document.getElementById("DD01"); // input field for question DD01 var question = document.getElementById("DD02_qst"); // question DD02 to be shown/hidden function toogle() { if (dropdown.value == "7") { // enter the value (answer code) here, which should insert the second drop-down question.style.display = ""; } else { question.style.display = "none"; } } SoSciTools.attachEvent(dropdown, "change", toogle); // adjust display when there is change in selection SoSciTools.attachEvent(dropdown, "click", toogle); // also check by clicking - otherwise the change will maybe only take effect when exiting the drop-down toogle(); // and also ensure the correct display at the beginning // --> </script>
Example 3: Alternative Questions
You have a drop-down selection “AB05” and want to offer a further selection depending on the selection. In this example, another selection (place of interest/sight) must be created next to the first selection (favourite city) for every city and included on the page in order to do this.
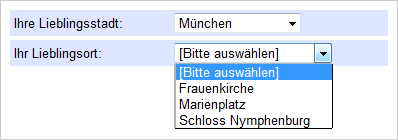
Tip: If you also take a visible selection into consideration, Extended Selections facilitate a hierarchical selection of options in a dynamic version already.
Tip: The dynamic display of questions also works in combination with Placing Questions Side by Side.
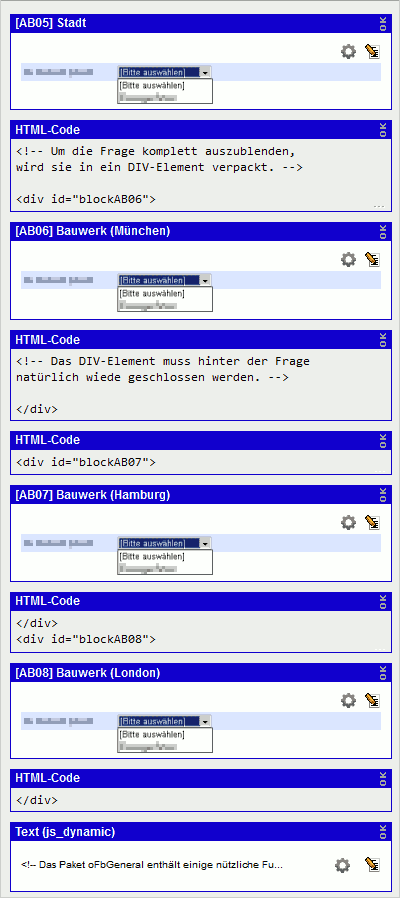
Questionnaire Page
Perhaps you cannot work with the standard HTML IDs available – because you integrate a question multiple times on the page for some of them and display different items for each one. In this instance, the questions to be shown are enclosed with DIV elements. The questionnaire page will be rather long as result of this. For the first question, 4 pixels is set as the Spacing to the next question ( ).
).
JavaScript Code
The following HTML/JavaScript code is saved in a text element (e.g. with the ID “js_dynamic”, display: “HTML-Code”):
<script type="text/javascript"> <!-- var dropdown = document.getElementById("AB05"); function blender() { // The value whose value corresponds to the answer code in the Variables Overview var selected = dropdown.value; // However, the value is text rather than a number selected = parseInt(selection); // This check is repeated for each question to be shown var question1 = document.getElementById("blockAB06"); if (selected == 1) { // show question1.style.display = ""; } else { // hide question1.style.display = "none"; } var question2 = document.getElementById("blockAB07"); if (selected == 2) { question2 .style.display = ""; } else { question2 .style.display = "none"; } var question3 = document.getElementById("blockAB08"); if (selected == 3) { question3 .style.display = ""; } else { question3 .style.display = "none"; } } // The function should be called up first directly // All drop-downs have to be hidden blender(); // Now the function still has to be linked with the change event // of the first drop-down SoSciTools.attachEvent(dropdown, "change", blender); SoSciTools.attachEvent(dropdown, "click", blender); // --> </script>
Beispiel 4: Skala
In this example, a scale item with 5 options (1=“not at all” to 5=“very often”) is to be linked to text fields. The text field for each item should only appear if the option 3, 4 or 5 has been selected.
Furthermore, the solution shall not only be used for a pair of items, but for a whole battery (10 scale items and 10 text input fields, which are represented as Combined Questions). To make this work without having to repeat the whole code 10 times, the JavaScript functionality is encapsulated as a class (function). This class is then called exactly once for each of the 10 items.
In the following example, the items have the following identifiers:
- Scales: SK01_01 to SK01_10
- Text inputs: TE01_01 to TE01_10
The JavaScript code for the 10 item pairs would look like this. A large part of the code is spent on first finding the selection fields of each scale item (at the top). This has the advantage that the code works independent of the scale level and of DK options.
The core of the function, which shows and hides the input field, is again the element.style.display = "none";
<script type="text/javascript"> /** * Find and list inputs (radio) of the * scale with the identifier itemID. */ function getScaleInputs(itemID) { var inputs = {}; // The regular inputs for (var i=1; i<100; i++) { var inputID = itemID + i; var input = document.getElementById(inputID); if (input) { inputs[i] = input; } else { break; } } // And then there may be DK options for (var i=-1; i>=-3; i--) { var inputID = itemID + "DK" + (-i); if (i == -1) { inputID = itemID + "DK"; } var input = document.getElementById(inputID); if (input) { inputs[i] = input; } } return inputs; } /** * The class that connects the scale item (identifier itemID) * to a text input (or similar) with the identifier inputID. * The array "show" defines for which values the * input field or item should be displayed. */ function linkScaleToInput(itemID, inputID, show) { // First, we need all radio inputs for the item var radio = getScaleInputs(itemID); var element = document.getElementById(inputID); // We need a function to read the value // that was checked in the scale function getValue() { for (var value in radio) { if (radio[value].checked) { return parseInt(value); } } return -9; } // Then we need a function to respond // to the selection function onSelect() { var value = getValue(); // Display, if the value is listed in "show", // or hife vial display=none if (show.indexOf(value) > -1) { element.style.display = ""; } else { element.style.display = "none"; } } for (var value in radio) { radio[value].addEventListener("click", onSelect); } // Use the correct display in the beginning onSelect(); } // One instanmce of the class for each scale item new linkScaleToInput("SK01_01", "TE01_01", [3,4,5]); new linkScaleToInput("SK01_02", "TE01_02", [3,4,5]); new linkScaleToInput("SK01_03", "TE01_03", [3,4,5]); new linkScaleToInput("SK01_04", "TE01_04", [3,4,5]); new linkScaleToInput("SK01_05", "TE01_05", [3,4,5]); new linkScaleToInput("SK01_06", "TE01_06", [3,4,5]); new linkScaleToInput("SK01_07", "TE01_07", [3,4,5]); new linkScaleToInput("SK01_08", "TE01_08", [3,4,5]); new linkScaleToInput("SK01_09", "TE01_09", [3,4,5]); new linkScaleToInput("SK01_10", "TE01_10", [3,4,5]); </script>
